C-IDS: Solving Contextual POMDP via Information-Directed Objective

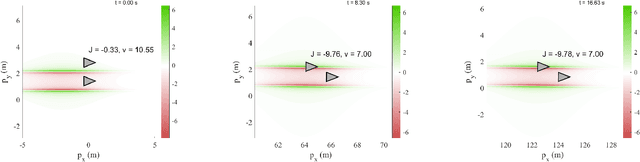
We study the policy synthesis problem in contextual partially observable Markov decision processes (CPOMDPs), where the environment is governed by an unknown latent context that induces distinct POMDP dynamics. Our goal is to design a policy that simultaneously maximizes cumulative return and actively reduces uncertainty about the underlying context. We introduce an information-directed objective that augments reward maximization with mutual information between the latent context and the agent's observations. We develop the C-IDS algorithm to synthesize policies that maximize the information-directed objective. We show that the objective can be interpreted as a Lagrangian relaxation of the linear information ratio and prove that the temperature parameter is an upper bound on the information ratio. Based on this characterization, we establish a sublinear Bayesian regret bound over K episodes. We evaluate our approach on a continuous Light-Dark environment and show that it consistently outperforms standard POMDP solvers that treat the unknown context as a latent state variable, achieving faster context identification and higher returns.

Target Defense against Sequentially Arriving Intruders

We consider a variant of the target defense problem where a single defender is tasked to capture a sequence of incoming intruders. The intruders' objective is to breach the target boundary without being captured by the defender. As soon as the current intruder breaches the target or gets captured by the defender, the next intruder appears at a random location on a fixed circle surrounding the target. Therefore, the defender's final location at the end of the current game becomes its initial location for the next game. Thus, the players pick strategies that are advantageous for the current as well as for the future games. Depending on the information available to the players, each game is divided into two phases: partial information and full information phase. Under some assumptions on the sensing and speed capabilities, we analyze the agents' strategies in both phases. We derive equilibrium strategies for both the players to optimize the capture percentage using the notions of engagement surface and capture circle. We quantify the percentage of capture for both finite and infinite sequences of incoming intruders.

A Constraint-Driven Approach to Line Flocking: The V Formation as an Energy-Saving Strategy

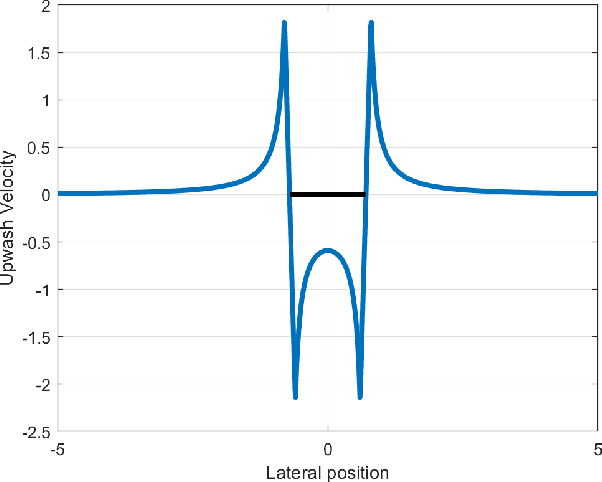
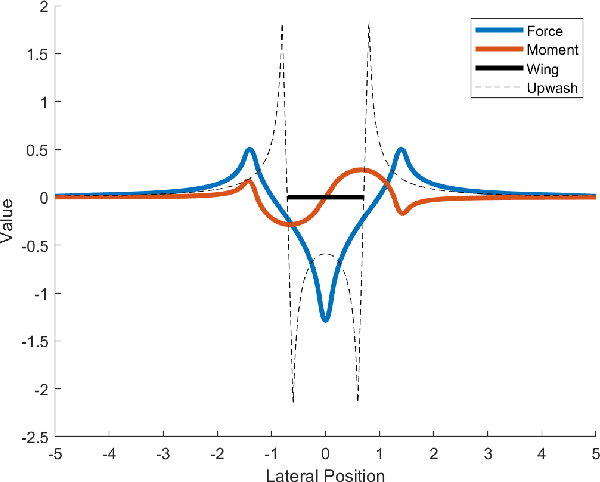
The study of robotic flocking has received significant attention in the past twenty years. In this article, we present a constraint-driven control algorithm that minimizes the energy consumption of individual agents and yields an emergent V formation. As the formation emerges from the decentralized interaction between agents, our approach is robust to the spontaneous addition or removal of agents to the system. First, we present an analytical model for the trailing upwash behind a fixed-wing UAV, and we derive the optimal air speed for trailing UAVs to maximize their travel endurance. Next, we prove that simply flying at the optimal airspeed will never lead to emergent flocking behavior, and we propose a new decentralized "anseroid" behavior that yields emergent V formations. We encode these behaviors in a constraint-driven control algorithm that minimizes the locomotive power of each UAV. Finally, we prove that UAVs initialized in an approximate V or echelon formation will converge under our proposed control law, and we demonstrate this emergence occurs in real-time in simulation and in physical experiments with a fleet of Crazyflie quadrotors.

Survey of Recent Multi-Agent Reinforcement Learning Algorithms Utilizing Centralized Training

Much work has been dedicated to the exploration of Multi-Agent Reinforcement Learning (MARL) paradigms implementing a centralized learning with decentralized execution (CLDE) approach to achieve human-like collaboration in cooperative tasks. Here, we discuss variations of centralized training and describe a recent survey of algorithmic approaches. The goal is to explore how different implementations of information sharing mechanism in centralized learning may give rise to distinct group coordinated behaviors in multi-agent systems performing cooperative tasks.

Differential Flatness as a Sufficient Condition to Generate Optimal Trajectories in Real Time

As robotic systems increase in autonomy, there is a strong need to plan efficient trajectories in real-time. In this paper, we propose an approach to significantly reduce the complexity of solving optimal control problems both numerically and analytically. We exploit the property of differential flatness to show that it is always possible to decouple the forward dynamics of the system's state from the backward dynamics that emerge from the Euler-Lagrange equations. This coupling generally leads to instabilities in numerical approaches; thus, we expect our method to make traditional "shooting" methods a viable choice for optimal trajectory planning in differentially flat systems. To provide intuition for our approach, we also present an illustrative example of generating minimum-thrust trajectories for a quadrotor. Furthermore, we employ quaternions to track the quadrotor's orientation, which, unlike the Euler-angle representation, do not introduce additional singularities into the model.